이 문제는 거의 2일?
적게 생각하긴 했지만.. 계속 생각해도 생각이 나지 않아 엄청 답답해 하고 있었다..
그러다 결국 오늘 글을 쓰기 위해 유튜브를 급히 보았다.
세상.. 엄청 똑똑하신 분들이 많던데.. 보다가 엄청 띠용하는 분의 영상을 보고 설명을 해보고자 한다.
DP란 결국 규칙성을 찾는 문제인데 규칙성 찾기가 너무나 어렵다 ㅠㅠ
우선 문제는 다음과 같다
가장 적은 개수의 봉지로 설탕을 나누기 위해서는 5봉지가 많아야 된다.
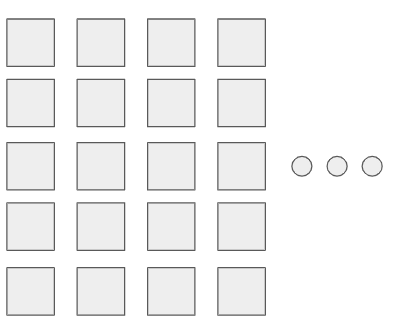
그래서 설탕을 5개씩 나열해보면 위 그림과 같이 나열 할 수 있다.
그럼 5개로 나누었을 때 경우의 수는
설탕이 0개, 1개, 2개, 3개, 4개가 남는 경우가 있다.
그림으로 표현하면

이러한 경우가 있다.
이때를 봉지로 계산해보면!

한개의 설탕이 남는 경우, 위와 같이 5개의 봉지로 나눈 설탕을 1봉지에서 뺀 뒤 3봉지 2개로 만들 수 있다.
이를 수식으로 표현하면, (5개의 봉지 개수 - 1 + 3개봉지 2개)
이런식으로 계산을 하게 되면

위와 같은 모양이 나오는 것을 알 수 있습니다.
5개로 묶은 봉지의 개수를 X라고 하고, 이를 표로 정리하게 되면
| 5묶음 | 3묶음 | 총 개수 | |
| 0 | X | 0 | X |
| 1 | X-1 | 2 | X+1 |
| 2 | X-2 | 4 | X+2 |
| 3 | X | 1 | X+1 |
| 4 | X-1 | 3 | X+2 |
가 됩니다.
그런데 이때 중요한 조건이 한가지 있습니다.
| 1 | X-1 | 2 | X+1 |
| 2 | X-2 | 4 | X+2 |
| 4 | X-1 | 3 | X+2 |
이 세가지의 경우, 봉지의 개수를 표현하는 것 이기 때문에 빨간색으로 표시한 부분의 수가 양수여야만 합니다.
이를 종합적으로 코드로 나타내게 되면,
이 됩니다.
유튭 덕분에 한 번에 패쑤!

DP 문제라고 해서 엄청 엄청 복잡하게 생각했는데, 이렇게 간단하게 생각할 수도 있다니 너무 놀라웠다..
DP라고해서 복잡한 방법이 아니라 경우의 수를 생각해서 좀 더 간단히 표현하는 방법을 익혀야겠다.
끄읐!~!
'ALGORITHM > Java algorithm' 카테고리의 다른 글
| [백준] 1655번 가운데를 말해요 (2) | 2021.01.17 |
|---|---|
| [백준] 12865번 평범한 배낭 (0) | 2021.01.13 |
| [백준] 11726번 타일 채우기 (0) | 2020.10.26 |
| [백준] 10773번 제로 Java (0) | 2020.10.20 |
| [백준] 9625번 BABBA Java (0) | 2020.10.19 |