오랜만에 새해 다짐으로 했던 알고리즘 문제를 풀었다.
근데 첫 문제부터 난관..
시작부터 나에게 고난을 준 문제는 아래에 있다.

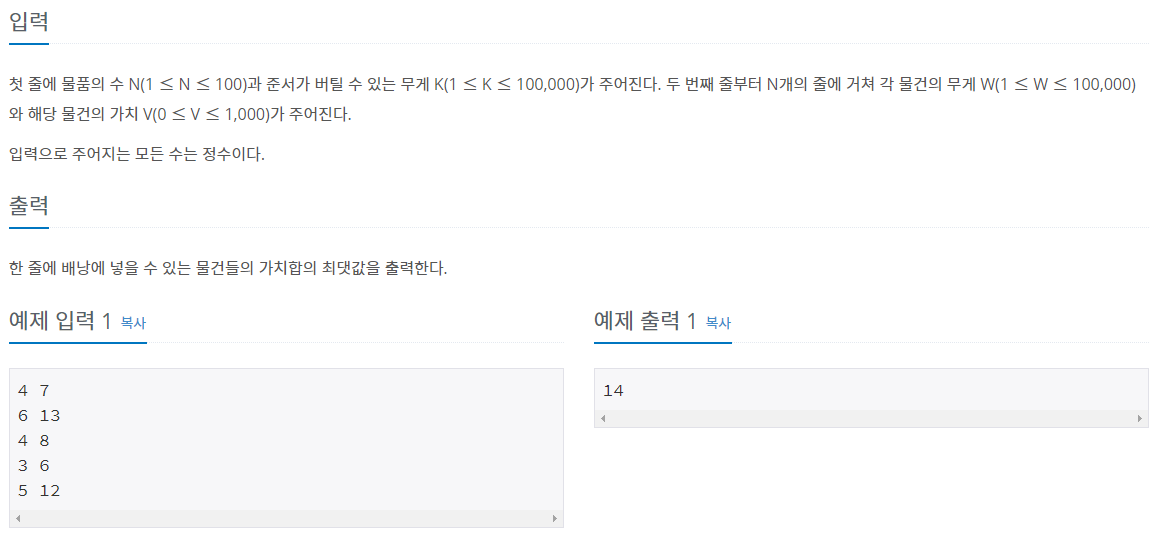
이 문제를 보고 나는 DP라는 것을 알았지만.. 메모이제이션/냅색 방법이라고는 생각도 못했다..
그래서 내가 처음에 도전한 방법은
한 무게당 n * n-1 * n-2 ... 개를 하나하나 비교해보는 방식이었다.
근데 이 방법으로 짜는 것도 java로 하려니 너무너무 어려웠다.
C/C++ 에서는 지역 변수가 따로 있어서 가능 할 것 같았는데, 여기서는 지역도 전역처럼 되어 버려서.. 너무 어려워@_@
내가 생각해낸 코드이다.
근데 이 코드가 안되서.. 조금 더 수정하면 될 것 같아서 아직 가지고 있는 중이다..
수정해봐야지~!
그 후에 고민해보다가
구글링을 통해 알고리즘을 찾았다.
바로바로
메모이제이션 냅색 알고리즘!
이 알고리즘 이름은 졸업하고 진짜 처음 듣는 것 같다..
거의 3년만 허허..
그만큼 공부를 안했다는 사실에 너무 부끄럽고 슬펐다.
일단 알고리즘 설명!
위의 예시로 설명을 하겠다.
일단 내가 받은 입력을 표로 정리하면 아래와 같다.
| 종류 | 무게 | 가치 |
| N1 | 6 | 13 |
| N2 | 4 | 8 |
| N3 | 3 | 6 |
| N4 | 5 | 12 |
이제 무게별로 최대 가치를 정리를 해보자.
STEP 1.
처음에는 다 0으로 채워준다.
| 종류 / 무게 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| N0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
STEP 2.
최대 무게가 N의 무게보다 작을 경우, 계산해주지 않는다.
| 종류 / 무게 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| N0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
STEP 3.
최대 무게가 N의 무게보다 크거나 같을 경우, 계산을 해준다.
이때 최대 무게 = 3 , N의 무게 = 3 -> 가치=6이므로 6을 적어준다.
이때 N보다 아래의 있는 N도 같은 무게를 적어준다.
왜냐하면, N4의 무게는 5로 5가 올때까지는 N3의 가치를 지니고 있어야 하기 때문이다.
| 종류 / 무게 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| N0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N3 | 0 | 0 | 0 | 6 | 0 | 0 | 0 | 0 |
| N4 | 0 | 0 | 0 | 6 | 0 | 0 | 0 | 0 |
STEP 4.
최대무게 = 4 의 경우, N2의 무게 = 4 이므로 N2의 가치를 적어 줄 수 있다.
아래 N3, N4의 가치들도 N2의 가치를 지니게 된다.
| 종류 / 무게 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| N0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N2 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 |
| N3 | 0 | 0 | 0 | 6 | 8 | 0 | 0 | 0 |
| N4 | 0 | 0 | 0 | 6 | 8 | 0 | 0 | 0 |
STEP 5.
최대무게 = 5 의 경우, N4의 무게 = 5 이므로 N4의 가치를 적어 줄 수 있다.
| 종류 / 무게 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| N0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N2 | 0 | 0 | 0 | 0 | 8 | 8 | 0 | 0 |
| N3 | 0 | 0 | 0 | 6 | 8 | 8 | 0 | 0 |
| N4 | 0 | 0 | 0 | 6 | 8 | 12 | 0 | 0 |
STEP 6.
최대무게 = 6 의 경우, N1의 무게 = 6 이므로 N1의 가치를 적어 줄 수 있고
N2, N3, N4도 해당 가치를 가지게 된다.
| 종류 / 무게 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| N0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N1 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 0 |
| N2 | 0 | 0 | 0 | 0 | 8 | 8 | 13 | 0 |
| N3 | 0 | 0 | 0 | 6 | 8 | 8 | 13 | 0 |
| N4 | 0 | 0 | 0 | 6 | 8 | 12 | 13 | 0 |
STEP 7.
최대무게 = 7 의 경우,
N2 일때 남은 무게가 최대무게 (7) - N2의 무게(4) 로 3의 무게가 남게 된다.
이때, 남은 무게3은 N3의 무게가 된다.
여기서 N2의 가치는 두 가지를 선택 할 수 있다.
- 1. N2의 무게 4일 때의 가치 + 남은 무게(N3)의 가치 -> 14
- 2. N1의 가치 -> 13
이 중에 큰 것으로 정하면 되는데, 첫 번째 경우가 크므로 14의 가치를 갖게 된다.
N3, N4도 같은 가치를 갖게 된다.
| 종류 / 무게 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| N0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N1 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 13 |
| N2 | 0 | 0 | 0 | 0 | 8 | 8 | 13 | 14 |
| N3 | 0 | 0 | 0 | 6 | 8 | 8 | 13 | 14 |
| N4 | 0 | 0 | 0 | 6 | 8 | 12 | 13 | 14 |
따라서 마지막 출력은
DP[n][k]를 하면 된다.
이를 정리한 소스는 아래와 같다.
나의 결과!

관련 문제를 더 풀어봐야겠다.
끄읏!
'ALGORITHM > Java algorithm' 카테고리의 다른 글
| [LeetCode][Java] 100. Same Tree (0) | 2022.09.01 |
|---|---|
| [백준] 1655번 가운데를 말해요 (2) | 2021.01.17 |
| [백준] 2839번 JAVA 설탕 배달 (0) | 2020.10.27 |
| [백준] 11726번 타일 채우기 (0) | 2020.10.26 |
| [백준] 10773번 제로 Java (0) | 2020.10.20 |